Final Project
Simulation driven slicing
Elevator Pitch/ Background
My project develops a streamlined workflow to convert complex simulation data into 3D printable models by segmenting surface meshes based on deformation data. My project will transform volumetric simulation outputs into surface meshes that can be directly used by slicing software, optimizing them for 3D printing. Demonstrated through a bike seat case study, this process will allow for precise control over infill densities, enhancing the final product’s functionality and comfort.
Motivtion
Simulations are crucial for predicting how a design will perform under real-world conditions. Many engineers use simulations to inform their design process. Additionally, Topology Optimization is being employed in real-world scenarios to optimize the geometry of objects with the goal of improving strength and reducing material usage. However, these methods are singularly focused on optimizing the geometry of an object. For instance, commercial software such as nTopology and Fusion360 now provide easy methods to perform simulation and optimization of designs, but they are primarily focused on geometry optimization.
In the application domain of 3D printing, slicing parameters such as infill density, temperatures, wall thickness, and many more can dramatically affect part performance. Therefore, it would be advantageous to control these parameters based on simulation results. However, the output data format used by simulation packages is not directly compatible with slicing software. These simulation packages can output their results in various formats, such as nodal displacements, temperatures, velocities, and pressure.
My project will explore a method to map these physical results to slicing settings. Specifically, this project addresses the challenge of translating volumetric simulation data into surface meshes that can be easily processed by slicing software to apply settings.
Implementation
Overview
The image below shows an overview of my project. The inputs of the workflow are a CAD model, in this case, a bike seat. The first section of the workflow involves meshing and simulation. I chose nTopology over ABAQUS because it was easier and quicker to use. nTopology is used to convert the CAD model into a volumetric mesh. Next, boundary conditions are applied to fix the bottom of the seat to the mount and apply a load to the top. The results of the simulation include a list of the vertices of the mesh and their displacements. I then export the mesh and the point map to separate files.
The next step involves code I wrote. My code reads in the volumetric mesh as a list of tetrahedrons. It then reads the displacement point map and matches each displacement with the correct point in the list of tetrahedrons. At this point, we have a list of tetrahedrons, each with 4 vertices. Each vertex contains an XYZ point along with a displacement. To slice this into submeshes, we need to be able to sample the displacement of arbitrary XYZ locations within the mesh. I will detail how my code can sample this data arbitrarily and how it maps displacements into a multi-material field later. I then use a custom version of the Marching Cubes algorithm that samples the volumetric field based on material distribution into segmented sub-meshes. Each mesh represents a certain range of displacement values (i.e. high, medium, low, none).
After exporting the sub-meshes, I import them into Prusa Slicer. I mate the sub-meshes together, along with the base mount, and assign materials. The mount gets assigned a hard PLA material, while the seat sub-meshes all get assigned soft TPU. To create the effect of multi-material-like behavior using only TPU, I assign different infill densities. The simulation indicates that the center of the seat is unsupported, so I assign a high infill density to create a stiffer region. The infills are graded such that they become softer as they move towards the ends of the seat. Once all the settings are applied, I can slice and print the object.
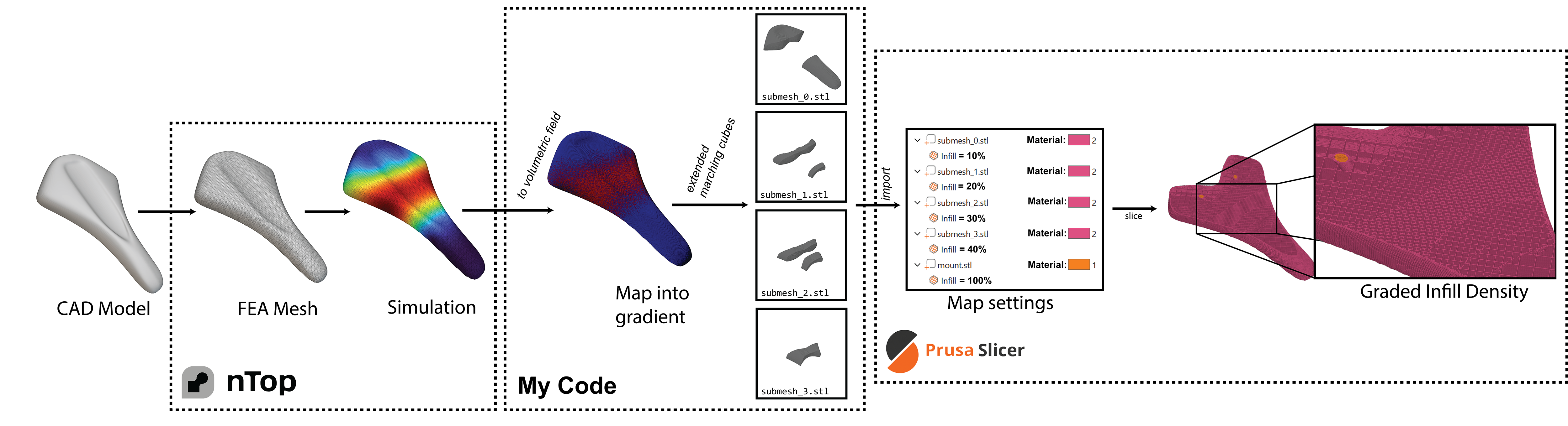
Simulation with nTopology
The video below shows the volumetric mesh computed by nTopology.
The image below shows the simulation setup and results. The purpose of this model is to demonstrate what happens when a seat is designed without sufficient support in the center of the mesh. The seat comprises two sub-parts: the body and the mount. The mount is treated as a undeformable bar affixed to the body, while the body is simulated as a TPU-printed object. I do not model contact in the simulation; instead, I fix the faces in the body that touch the mount. A downward force is applied to simulate a rider sitting on the body. From the simulation results, we can see significant deformation in the center of the body when a rider sits on it. Using this information, we will enhance the structural integrity by introducing higher-density infill to reduce deformation. However, this could compromise comfort in those areas, so a balance must be struck.
My Code: Converting Simulation Results into Segmented Meshes
My code operates on the output of a simulation, which comprises two main components stored in distinct data structures. It uses the original geometry in a finite element mesh. This mesh is constructed using tetrahedral triangular pyramid elements, effectively representing the surface and internal structure of the CAD model. The mesh’s resolution is chosen heuristically, balancing element count against computational demands. The mesh data is saved in an .INP file, consisting of two lists: one listing vertices with their respective XYZ coordinates, and another listing tetrahedral elements, where each node references a specific vertex from the former list. It’s important to note that vertices shared by multiple elements at intersections are included in the vertex list. My code reads this data into a corresponding C++ data structure. The second component of the simulation results is a displacement map. This text file mirrors the vertices from the mesh, each accompanied by a 3-component displacement vector indicating the node’s movement during simulation. My code processes this file along with the geometry from the .INP file, assigning the displacement vectors to their corresponding nodes.
At this point, we have a tetrahedral mesh, with each vertex associated with a displacement. Our next task involves the ability to sample any location within this mesh to determine both geometry and displacement. Initially, let’s focus on geometry. We aim to derive a function, g(x,y,z), where values greater than 0 signify locations outside the mesh, while values less than 0 indicate interior points. This function is known as point membership classification and serves to classify a given point’s position relative to the mesh. Within our tetrahedral mesh framework, we determine if a point is inside the mesh checking if it is contained within individual tetrahedrons. I will discuss a method for determining a point’s location within a tetrahedron later, for now, assume that it is a trivial process. Given this ability to determine if a point is within a tetrahedron, we iterate through all tetrahedrons in the mesh until we locate the one containing the point (or conclude it lies outside all tetrahedrons). However, this exhaustive approach disregards the spatial relationships among tetrahedrons, resulting in inefficiency.
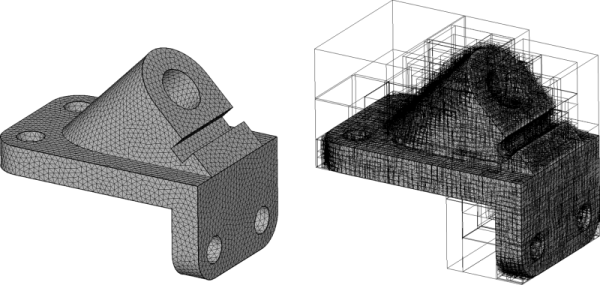
To streamline the process, we adopt an Axis-Aligned Bounding Box (AABB) Tree, a spatial data structure organizing geometric primitives hierarchically based on their spatial relationships. The construction of such a tree involves iteratively adding primitives and their bounding boxes, resulting in a binary tree structure encompassing all primitives. When checking whether a point resides within any primitive, we traverse the tree, benefiting from the efficiency of bounding box containment checks. The image below shows the processes of creating an AABB tree with triangles. The same processes can be extended to tetrahedrons. Although some tetrahedrons may require further point-in-tetrahedron tests due to overlapping bounding boxes, the overall process is very fast.
In my project, I use the AABB Tree implementation provided by the Computational Geometry Algorithms Library (CGAL). The image below is from the CGAL documentation and shows a visualized AABB Tree computed for a triangle surface mesh.
Using the AABB Tree we have rapid evaluation of the g(x,y,z) function. Next, we require a similar method for determining displacement at a given location. As displacement data is stored at each mesh vertex, we can use the AABB Tree to identify the tetrahedron containing a sampled point. However, this leaves us with four displacement vectors to choose from, one for each vertex of the tetrahedron. Instead of directly selecting the nearest vertex, which might work poorly for large tetrahedrons, we employ interpolation among the four vertices to obtain a displacement value best representing the sampled point’s position within the tetrahedron. The picture below shows this problem. The blue point is what we wish to sample.
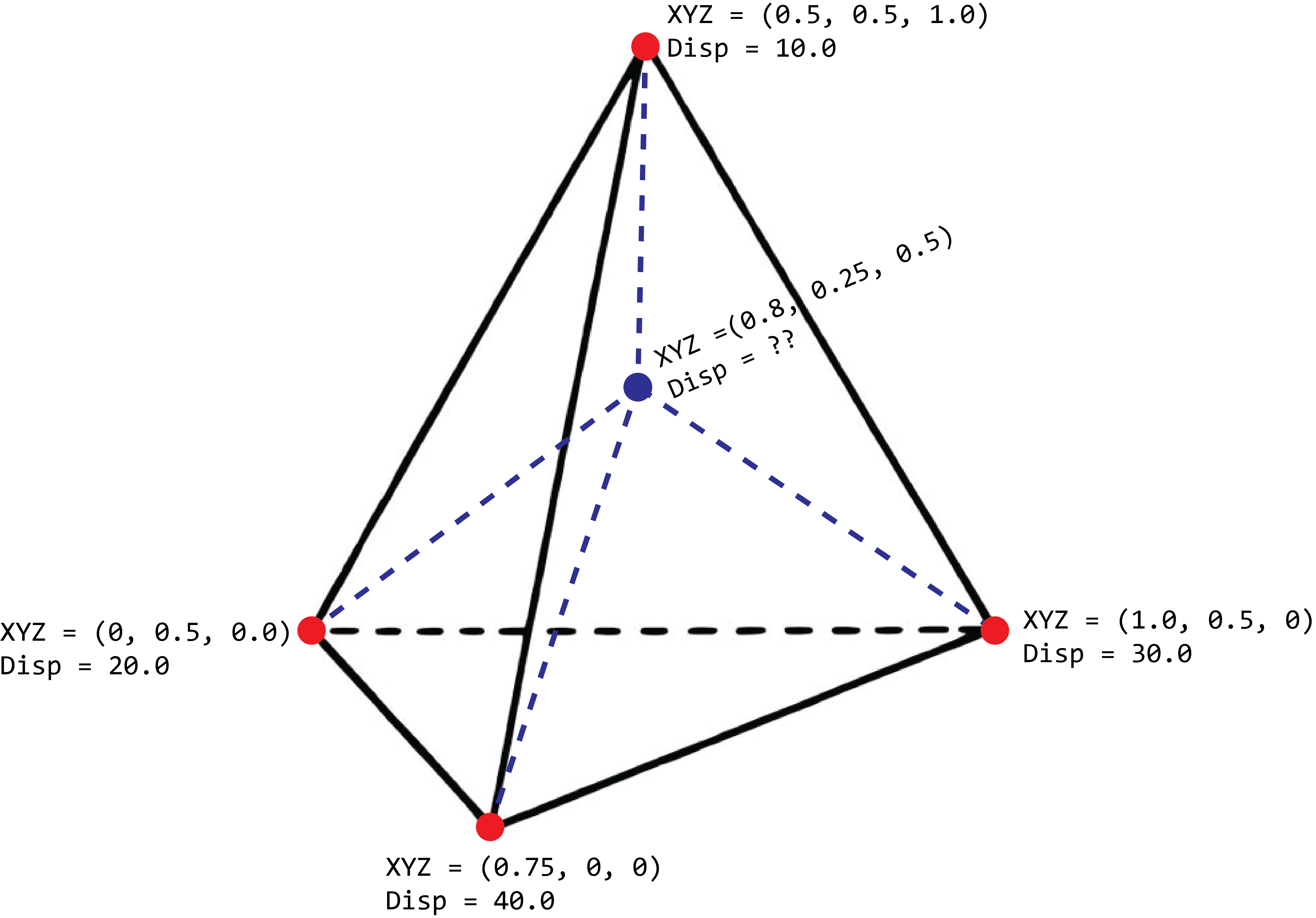
Tetrahedral interpolation involves computing the barycentric coordinates of the sampled point relative to the tetrahedron. Barycentric coordinates tell us where the sampled point is realative to each vertex. In the case of triangle, there are 3 components to its barycentric coordinates. In the case of a tetrahedron, there are 4 barycentric coordinates components. Multiplying these coordinates by the displacement vectors at each vertex yields an interpolated displacement vector. These barycentric coordinates not only facilitate interpolation, but can also be used to determine if a point is within the tetrahedron. A point lies outside the tetrahedron if any of its barycentric coordinate components fall outside the [0, 1] range.
Following tetrahedral interpolation, we obtain a displacement vector for a given location, yielding a function d(x,y,z) returning a 3-component displacement vector. The next step involves mapping this displacement vector to variable infill density. Users can specify a mathematical expression string returning infill density percentages between 0% and 100%, utilizing the magnitude variable. The magnitude variable is computed as the displacement vector’s length. This yields an expression of the form infill(x,y,z)=user_defined_expression_mapping * magnitude(d(x,y,z)). This function enables sampling at any location to retrieve the mapped infill density based on simulation results.
To connect everything together, we next need to convert our two functions, g(x, y, z) and infill(x, y, z) to triangulated surface meshes. We use a custom version of the marching cubes algorithm. This algorithm can convert signed distance fields into triangulated surface meshes and operates by dividing space into a grid of cubes. At each cube, it samples the geometric function g(x,y,z) at its eight vertices, leveraging a pre-defined lookup table to determine the surface’s intersection within the cube. If you are interested in more info, this video by Sebastian Lauge provides a great overview.
Originally proposed by Lorensen and Cline in 1987, the lookup table accounts for the 15 unique configurations of surface intersections possible with cubes. These configurations dictate the arrangement of triangles within each cube, ranging from none to five triangles. The picture below is from their original paper and shows the possible intersection configurations.

Our version of the algorithm expands beyond geometric surface reconstruction. We incorporate considerations for infill density segmentation using the infill(x,y,z) function. During corner sampling within each cube, we first compute the geometric function g(x,y,z) to determine if any vertex lies outside the mesh. If so, we mark the cube’s corners and move to the next cube. Conversely, a cube corner resides within the mesh, we sample the infill density function at that corner. By comparing the resulting infill density values against user-defined ranges, we selectively mark corners as inside or outside of the final mesh. This approach ensures the resulting triangulated mesh not only represents the object’s surface but also segments the object internally based on infill density. Users can specify the number of infill density regions and their corresponding ranges. These segmented meshes are next used to assign infill density in Prusa Slicer. The image below shows the output of my code when I slice the simulated model into four sub-meshes. Each of these meshes represents a certain range of deformation (intuitively: none, low, medium, and high).
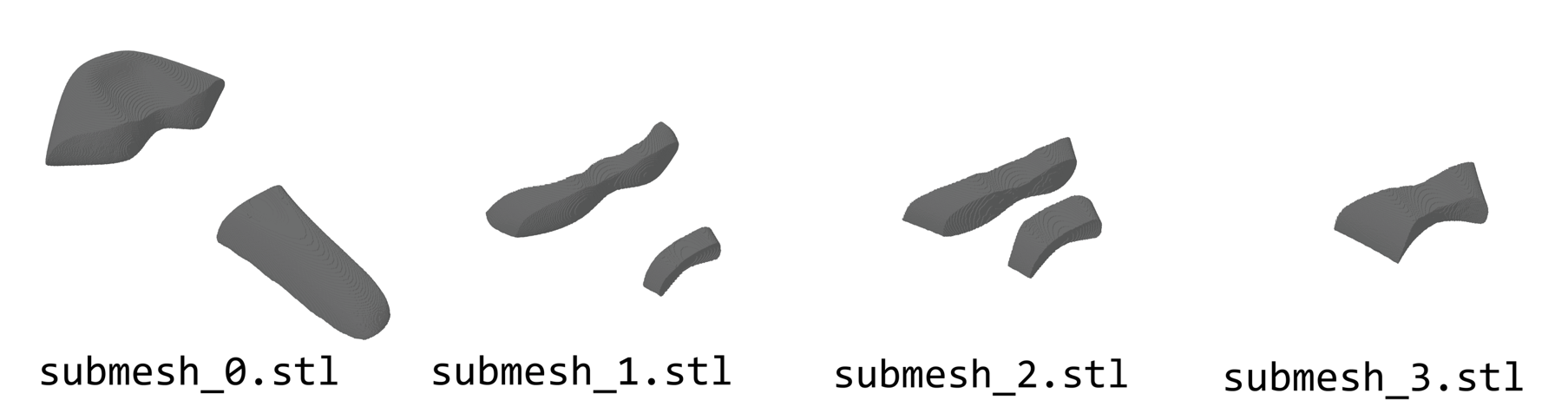
Preparting to Print with Prusa Slicer
I imported the sub-meshes into Prusa Slicer and allowed the program to treat them as a multi-material object. This ensures I can translate and rotate the object as a single unit. The image below shows how I can set the infill density for each sub-mesh. I assigned the same TPU material to each sub-mesh, while the mount received a hard PLA material. I also enabled supports to ensure stability during printing.

The images below show the sliced preview in prusa slice. From this you can see the graded infill pattern.


Printing the Seat
To print the bike seat, I used a soft TPU with a Shore hardness of 95A. Because TPU does not work well as a support material (given that it flexes), I used PLA for supports only. I originally intended to print the mounting bars underneath out of PLA, but they proved too brittle, so I skipped printing them. Below is a video time-lapse of the 26-hour print. You can see the two print heads swapping between PLA and TPU while printing. Once the print was done, the support material removed easily.
The Final Product
The full scale printed model is shown below.

The seat on the right was stopped halfway through the print to show a cutaway of the infill.



Code
I implemented my project using a few libraries. The project itself was implemented directly into a research package I have been developing called OpenVCAD. The OpenVCAD framework provided methods to render the designs and a basic structure. OpenVCAD works by having users “code” their objects similar to OpenSCAD. For my project, I implemented a new node type called a PointMap. The node takes parameters as PointMap(path_to_inp_file, path_to_displacement_map_csv, mapping_function_string) The point_map.h & point_map.cpp files contain most of the core data structure and algorithm. The code for segmenting meshes and exporting them is handled in mesh_exporter.cpp. The table below provides an overview of what libraries I used. The sections in bold are the code I wrote for this project. You can download the full-source code for my project here.
| Name | Description |
|---|---|
| AABB Tree Data Structure | Computational Geometry Algorithms Library (CGAL) |
| Visualization and Framework | OpenVCAD & QT |
| Math Expression Parsing | Exptrk Library |
| .INP and Point Map Loading | LoadTetrahedronsFromFile() in point_map.h & point_map.cpp |
| Core Algorithm | compute_displacement() in point_map.h & point_map.cpp |
| Tetrahedral Interpolation | tetrahedron.h |
| Modified Marching Cubes/ Segmenting | exportTreeToMaterialMesh() in mesh_exporter.cpp |
| .STL Saving | WriteSTLFile() in mesh_exporter.cpp |
Reflection
Overall, I felt that my project went well. I expected the modified marching cubes section to be hard and the simulation results loading to be easier. In the end, it was actually the reverse. Updating marching cubes to also segment based on the infill density regions was not too hard. The loading and sampling of the simulation results ended up being the bulk of my work. At first, my algorithm was checking every sample point against every tetrahedron in the mesh and was way too slow. I discovered the AABB tree and things improved a lot.
If I had more time, I would improve the surface finish on the exported meshes. If you look closely, you can see the individual cubes present from the marching cubes algorithm. This should not really be the case when we interpolate properly, but I was not able to get interpolation working with both the geometry and infill density being sampled. I have some ideas on how to fix it and will investigate those in the future. The other thing I plan to do is print the bike seat using multiple materials instead of infill regions. The difficulties with this are more on the printer side than the algorithm.