Large 1 - “Stringing Along”

Turtle and Lindenmayer Systems (L-Systems)

Task 1

Each section below shows the rendered image as well as the code that generates it.

Letter I

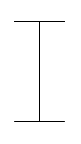
Letter T

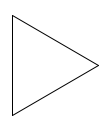
Triangle

Pentagon

Note: I wrote a generic polygon funciton. The pentagon can be generated with draw_polygon(100, 5)

Cicrle

The circle is drawn with 360 line segments

Task 2

The relevant code for completing the L-system is shown below. Specific code for each system is given in Task 3.

Draw Function for all L-systems

iterate()

numIterations

Task 3

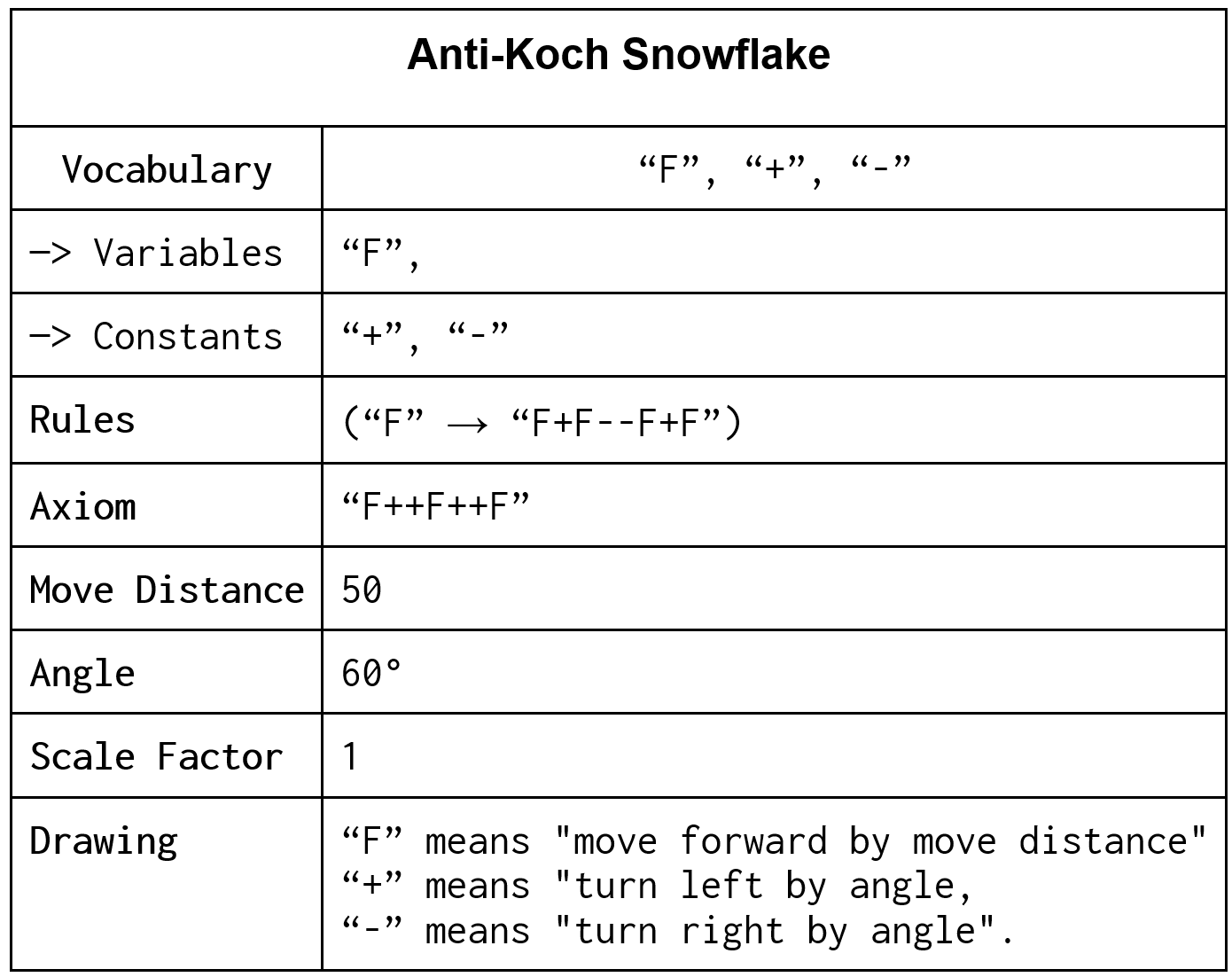
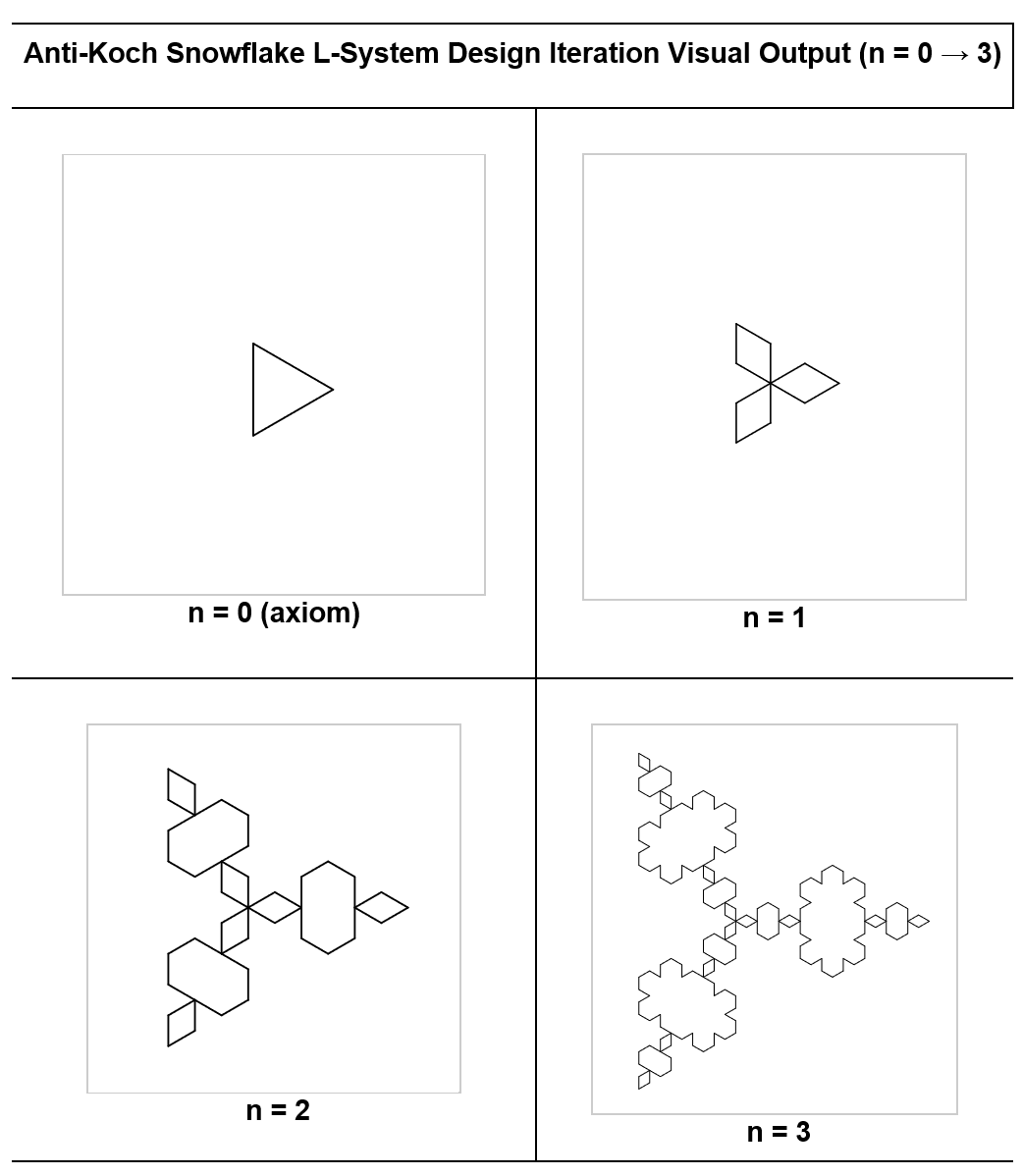
Design 1: Anti-Koch Snowflake

This design serves as the antithesis to the Koch snowflake. It was created by inverting all ‘+’ and ‘-‘ signs within the rules and axiom. The outcome is an unusual design that bears resemblance to a Koch snowflake, yet showcases a distinctive pattern.

Design Specification

Outputs

Code

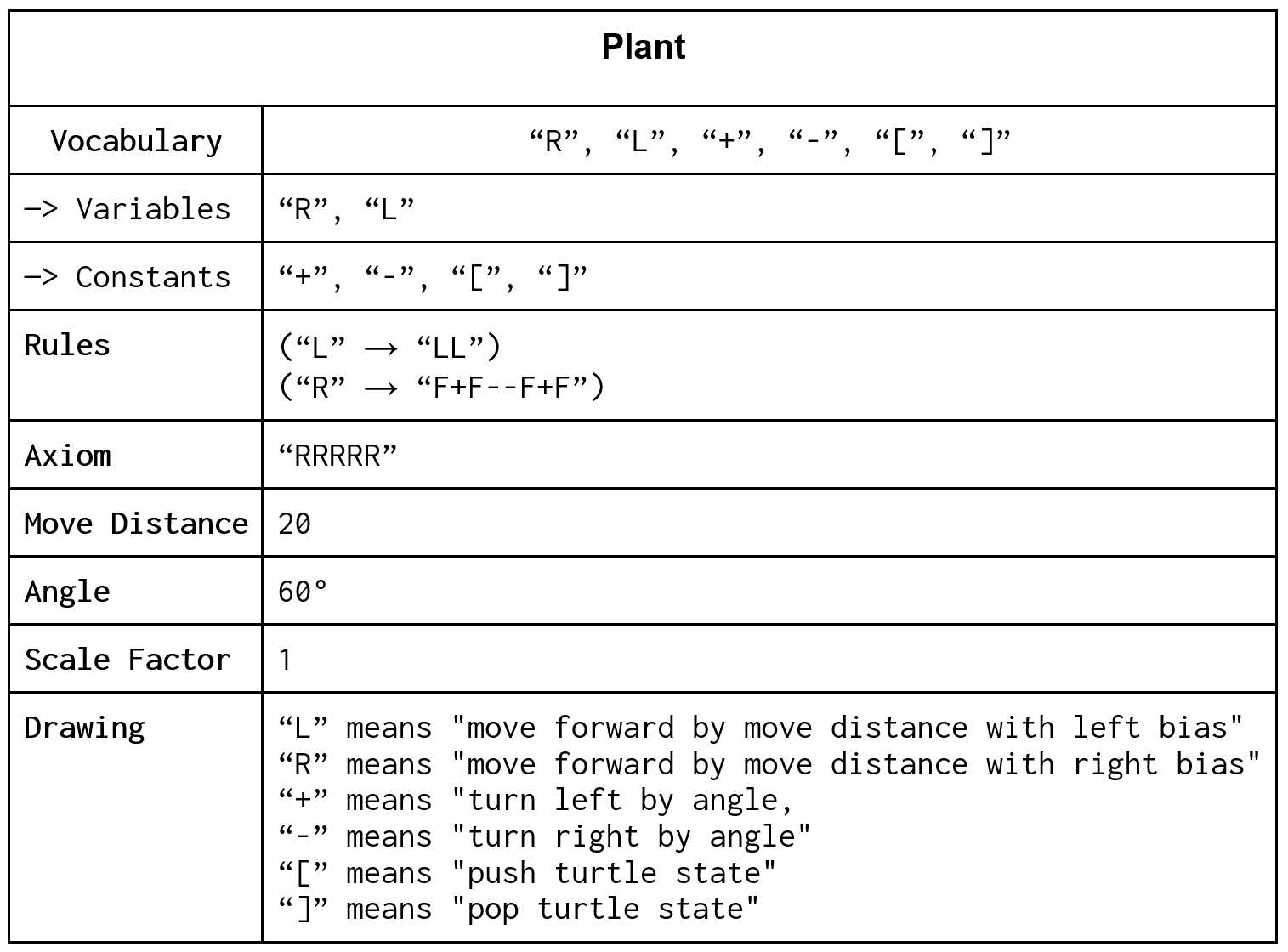
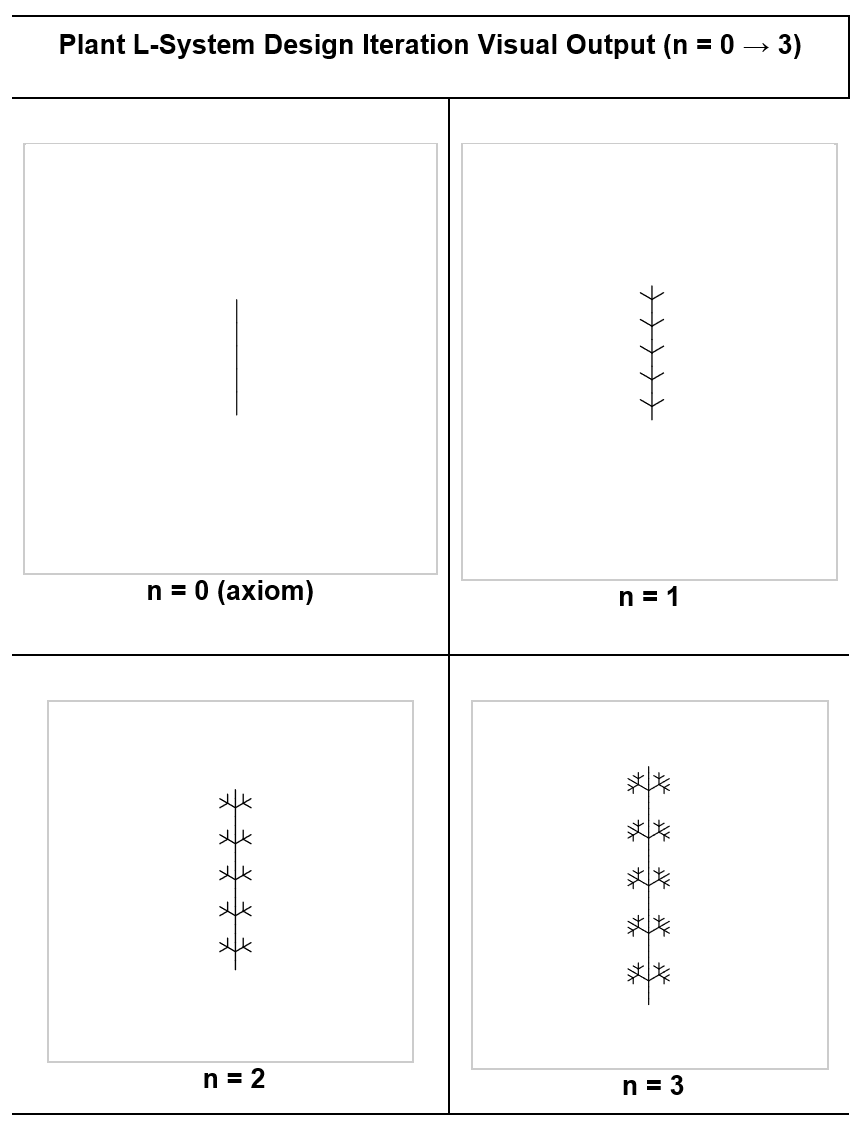
Design 2: Plant

This design simulates the growth of a plant, beginning with a stem. With each iteration, branches are added recursively.

Design Specification

Outputs

Code

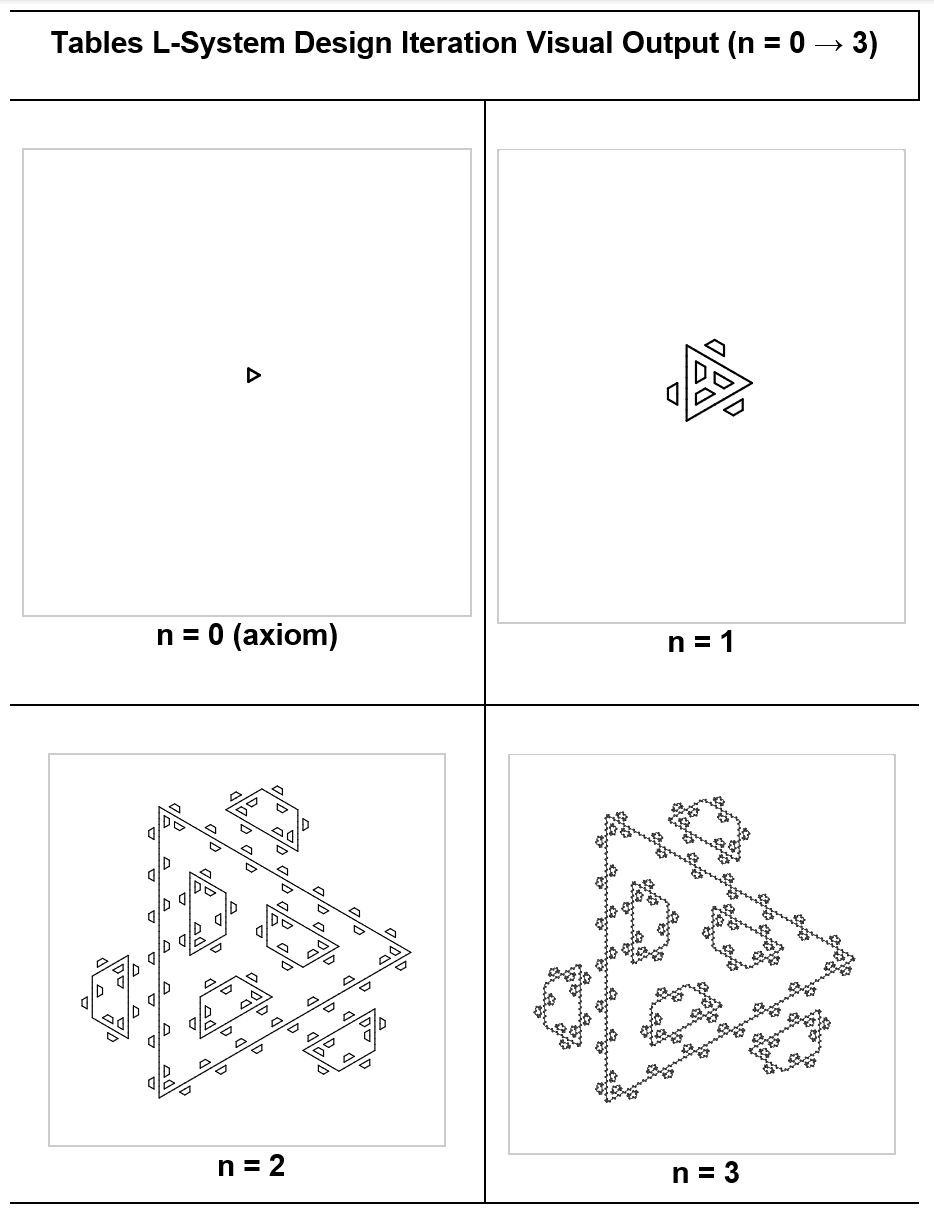
Design 3: Tables

I think this design resembles triangular tables surrounding triangular conference tables. As the number of iterations increases, more tables are recursively added.

Design Specification

Outputs

Note: Iteration n=3 is quite large and has been scaled down, resulting in less visible detail. In the scalable vector format, it appears fine but demands significant resources to render all the lines.

Code

Task 4

Both designs are made from 3mm acrylic. The designs were etched, and then cut out by a bounding box and triangle.

Anti-Koch Snowflake

Tables

Extra Credit

There are two primary methods for implementing stochasticity in L-systems. The first involves introducing randomness to the drawing function itself. This may include varying the distances for moving forward or the angles for rotation. I modified the LSystem constructor to accept ranges for distance and angle, generating random numbers within these bounds: ProbabilisticLSystem(String axiom, HashMap<Character, String[]> rules, float min_dist, float max_dist, float min_angle, float max_angle, float scaleFactor). Then I applied these ranges within the random function for both distance and angle:

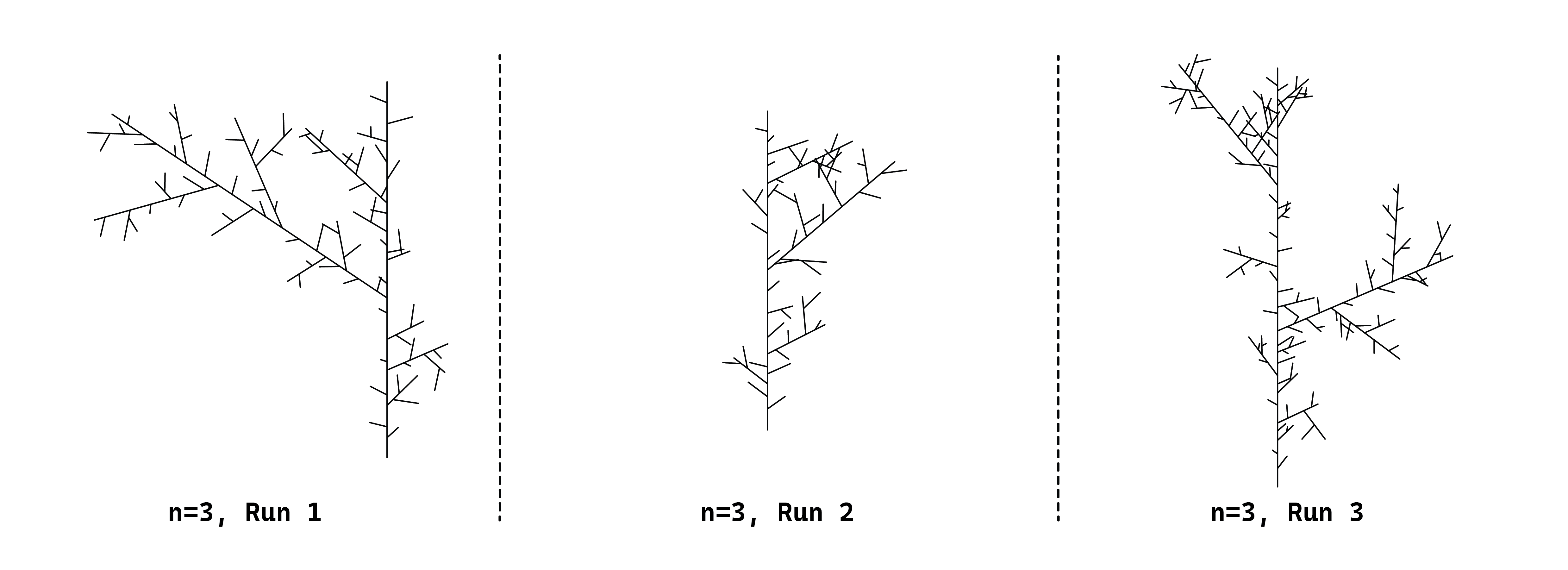
I modified the design based on the provided squares example but added random angles and distances. The code below demonstrates this definition. The image displays the same design executed three times for n=3, showcasing the randomness of the design.

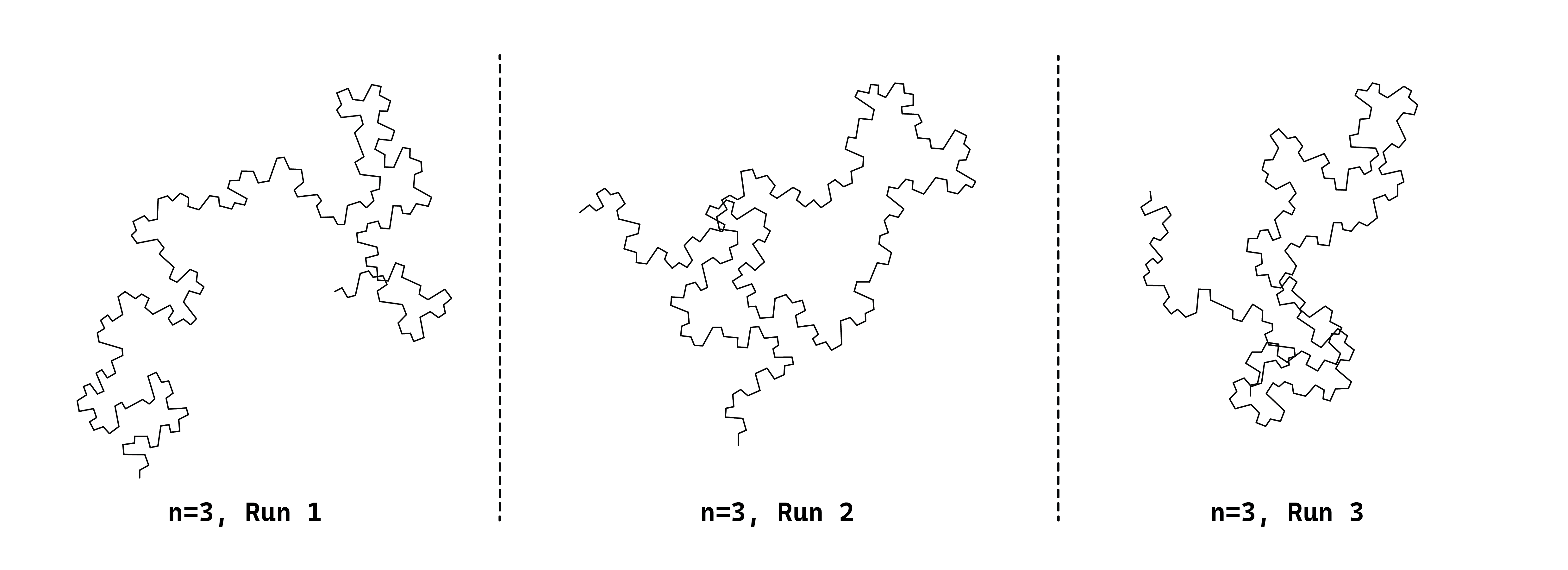
The alternative method for incorporating stochasticity in L-systems involves utilizing multiple rules for a single variable. The code below illustrates how this is achieved. I am using string arrays (String[]) to define multiple rules for a single variable. I updated the constructor to accommodate this feature. Additionally, I revised the iterate() function to access the array of strings and randomly select a rule to apply.

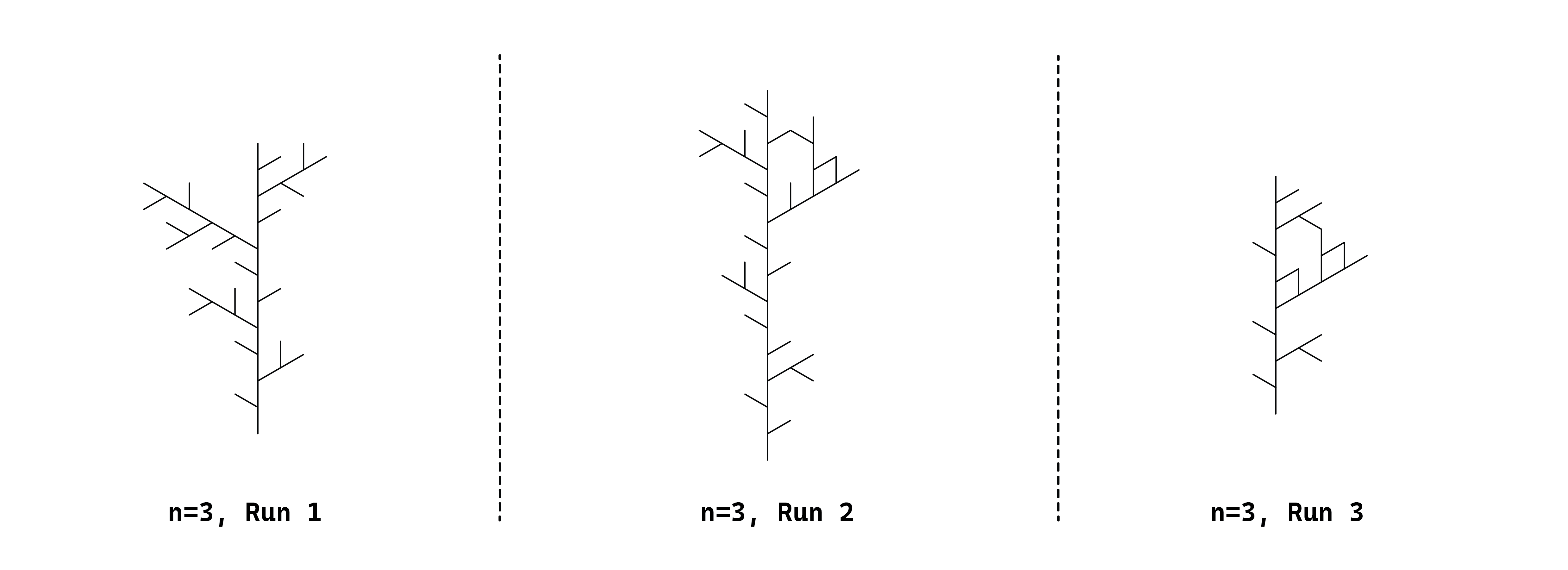
To demonstrate this, I created a plant design that uses forward, push, and pop commands. Two rules were established for the F variable. The stochastic L-system will randomly choose one of the two rules during each replacement. The code below presents the definition, and the image displays a demonstration of three runs of the same design.

Note: the distance and angle were fixed in this example

This final demonstration combines random distance, angle, and rule selection to create a more realistic plant representation.